22/2/22
20/2/22
DIÉDRICO. ÁNGULOS. VERDADERA MAGNITUD.
Contenidos relativos a ángulos para PEvAU. Andalucía
2019. EVAU. JUNIO EXTRAORDINARIA. DIÉDRICO ÁNGULOS
Determinar la verdadera magnitud del ángulo que forman dos planos.
Ángulos. Posiciones favorables. mongge
Ángulo que forma una recta con PV y PH mongge mongge
Ángulo que forma un plano con PV y PH. mongge
Ángulo que forma un plano con PV y PH ( aplicando cambio de plano). mongge
Plano que forma un ángulo determinado con PH. mongge
Ángulo que forma un plano con la línea de tierra. mongge
Ángulo entre recta y plano. mongge
Ángulo que forman dos rectas que se cortan. Por abatimiento del plano que las contiene. geogebra mongge1 mongge2 mongge3
14/2/22
DIÉDRICO. DISTANCIAS con geogebra y mongge
1. DISTANCIA ENTRE DOS PUNTOS. Verdadera mágnitud de un segmento.
geogebra por diferencia de cotas
geogebra por giro
geogebra por abatimiento
2. DISTANCIA PUNTO RECTA
mongge de un punto a una recta paralela a un plano de proyección
3. DISTANCIA PUNTO PLANO
mongge distancia de un punto a un plano proyectante
mongge distancia de un punto a un plano definido por una recta de máxima pendiente
mongge punto que diste una distancia d de un plano dado
mongge plano por el punto medio de un segmento
4. DISTANCIA ENTRE RECTAS PARALELAS
5. DISTANCIA ENTRE PLANOS PARALELOS
mongge plano paralelo a otro a una distancia determinada
24/1/22
23/1/22
2/11/21
11/6/21
3/5/21
INVERSIÓN. FIGURA INVERSA DE UNA CIRCUNFERENCIA.
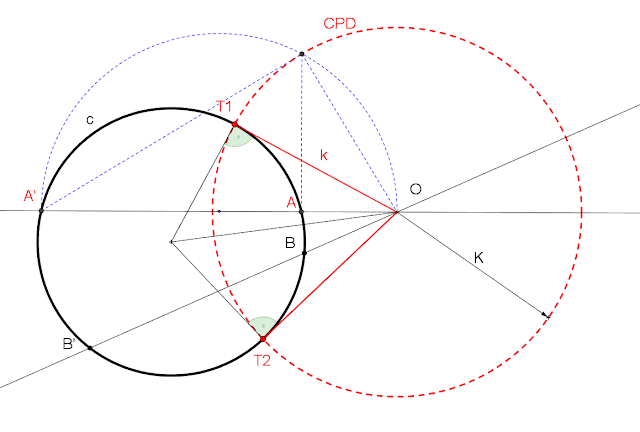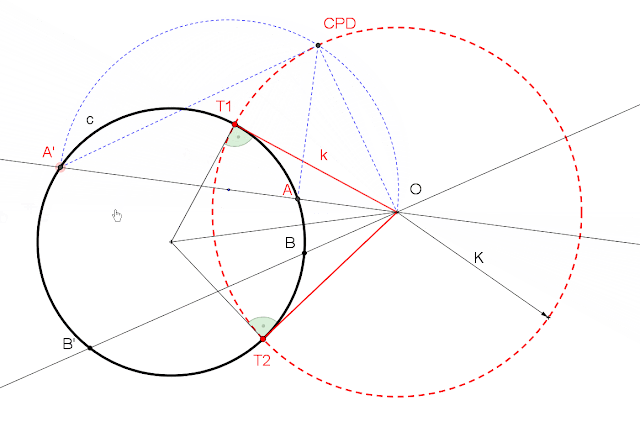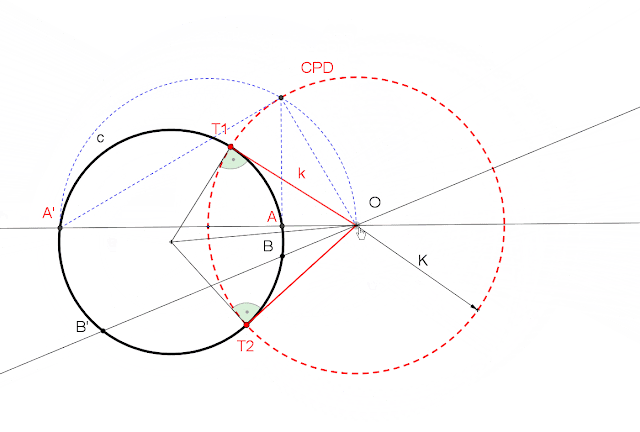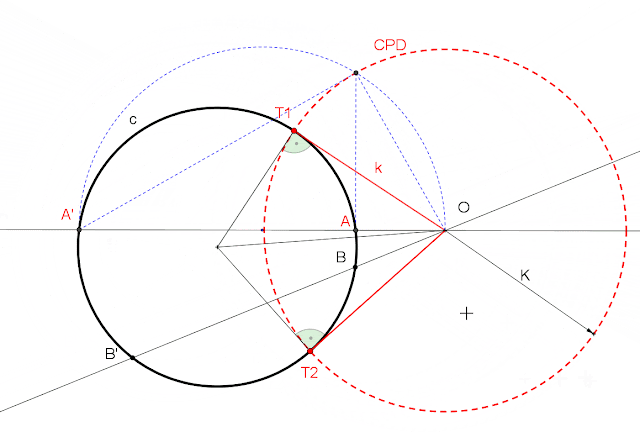
1. CIRCUNFERENCIA AUTOINVERSA.
Es ortogonal a la CPD, los únicos puntos dobles son los puntos de tangencia de las rectas trazadas desde el centro de inversión.
La CPD es una circunferencia autoinversa en la que todos sus puntos son dobles.
2. CIRCUNFERENCIA QUE NO PASA POR EL CENTRO DE INVERSIÓN.
Se transforma en otra circunferencia homotética.
Las parejas de puntos homotéticos no son parejas de puntos inversos, excepto los puntos de tangencia.
3. INVERSA DE UNA CIRCUNFERENCIA CONCÉNTRICA A LA CPD
2/5/21
INVERSIÓN. FIGURA INVERSA DE UNA RECTA
FIGURA INVERSA DE UNA RECTA QUE NO PASA POR EL CENTRO DE INVERSIÓN: se convierte en una circunferencia que sí pasa por el centro de inversión.
El centro de la circunferencia inversa tendrá su centro en la perpendicular a la recta desde el centro de inversión.
Si la recta es tangente a la CPD, la circunferencia también será tangente.
Si la recta corta a la CPD, la circunferencia pasará por los puntos de corte y el centro de inversión.
Si la recta pasa por el centro de inversión, se autoinvierte, se transforma en ella misma
4. RECTA QUE PASA POR EL CENTRO DE INVERSIÓN.