24/1/22
23/1/22
2/11/21
11/6/21
3/5/21
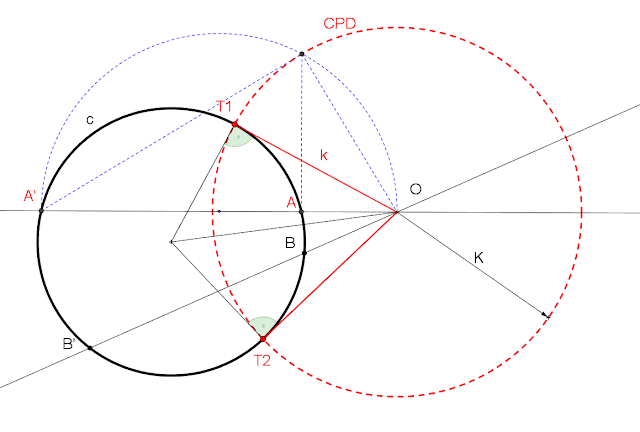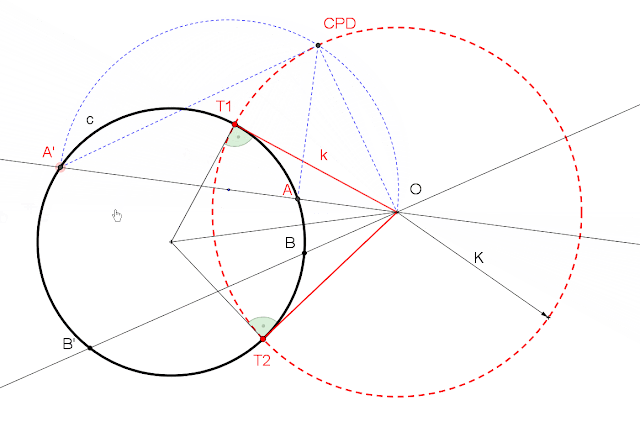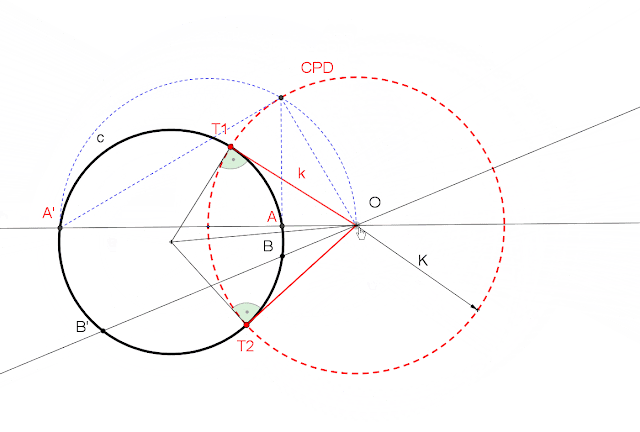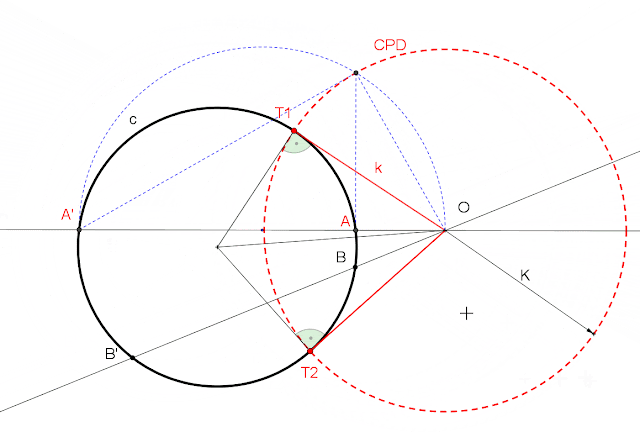
INVERSIÓN. FIGURA INVERSA DE UNA CIRCUNFERENCIA.
1. CIRCUNFERENCIA AUTOINVERSA.
Es ortogonal a la CPD, los únicos puntos dobles son los puntos de tangencia de las rectas trazadas desde el centro de inversión.
La CPD es una circunferencia autoinversa en la que todos sus puntos son dobles.
2. CIRCUNFERENCIA QUE NO PASA POR EL CENTRO DE INVERSIÓN.
Se transforma en otra circunferencia homotética.
Las parejas de puntos homotéticos no son parejas de puntos inversos, excepto los puntos de tangencia.
3. INVERSA DE UNA CIRCUNFERENCIA CONCÉNTRICA A LA CPD
2/5/21
INVERSIÓN. FIGURA INVERSA DE UNA RECTA
FIGURA INVERSA DE UNA RECTA QUE NO PASA POR EL CENTRO DE INVERSIÓN: se convierte en una circunferencia que sí pasa por el centro de inversión.
El centro de la circunferencia inversa tendrá su centro en la perpendicular a la recta desde el centro de inversión.
Si la recta es tangente a la CPD, la circunferencia también será tangente.
Si la recta corta a la CPD, la circunferencia pasará por los puntos de corte y el centro de inversión.
Si la recta pasa por el centro de inversión, se autoinvierte, se transforma en ella misma
4. RECTA QUE PASA POR EL CENTRO DE INVERSIÓN.
1/5/21
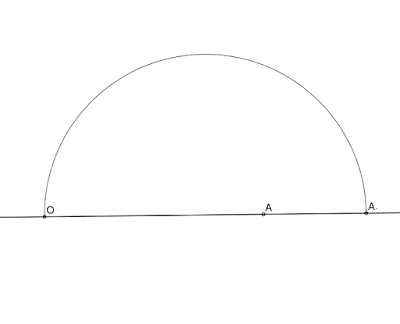
INVERSIÓN. Centro de inversión y pareja de puntos inversos
CENTRO DE INVERSIÓN Y UN PAR DE PUNTOS INVERSOS
OA X OA´= OT X OT
POTENCIA DE INVERSIÓN K: raiz cuadrada de OT X OT