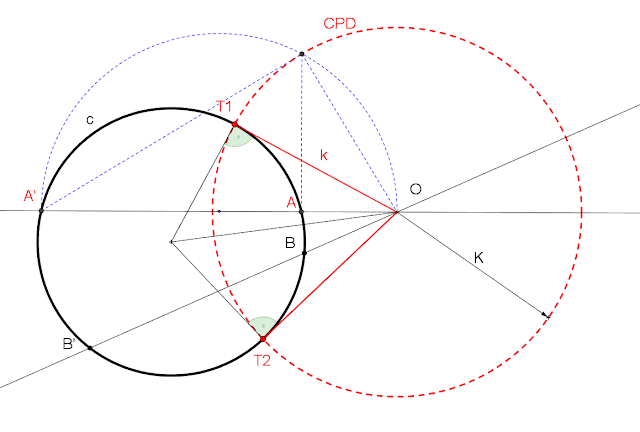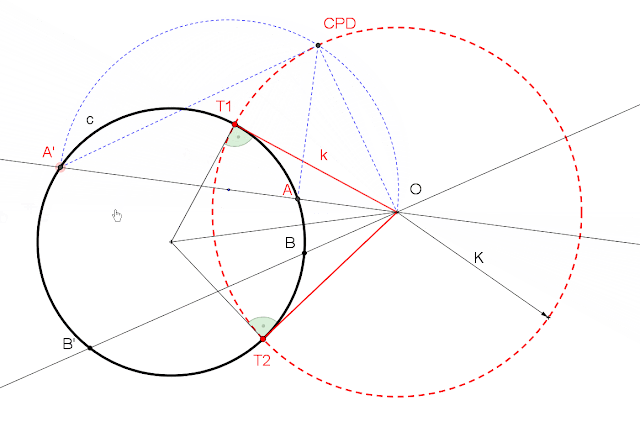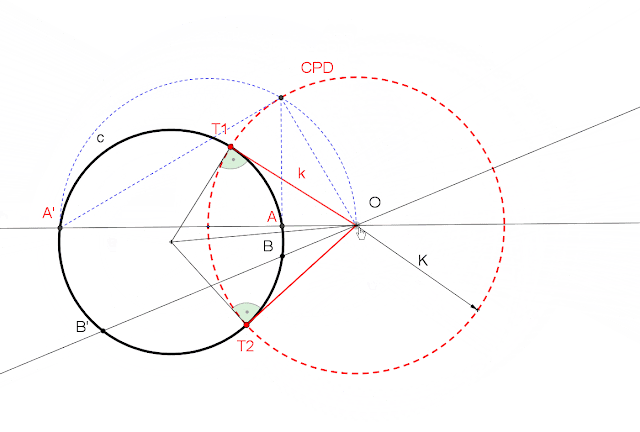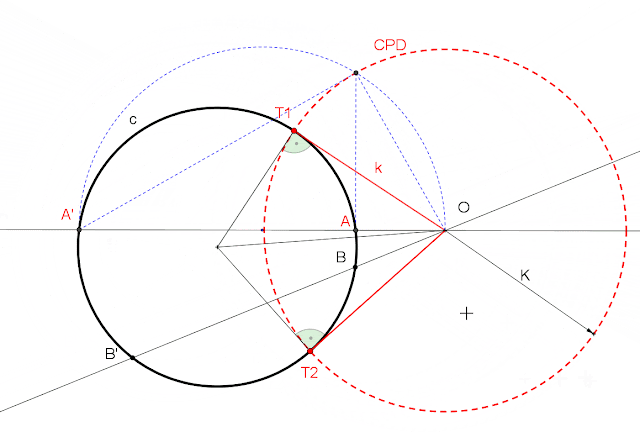
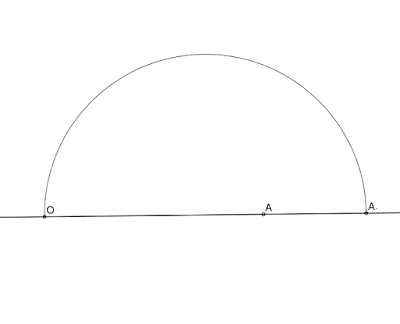
FIGURA INVERSA DE UNA RECTA QUE NO PASA POR EL CENTRO DE INVERSIÓN: se convierte en una circunferencia que sí pasa por el centro de inversión.
El centro de la circunferencia inversa tendrá su centro en la perpendicular a la recta desde el centro de inversión.
Si la recta es tangente a la CPD, la circunferencia también será tangente.
Si la recta corta a la CPD, la circunferencia pasará por los puntos de corte y el centro de inversión.
Si la recta pasa por el centro de inversión, se autoinvierte, se transforma en ella misma
1. RECTA EXTERIOR A LA CPD
perpendicular desde el centro de inversión a la recta r
se halla el inverso del punto A
La circunferencia inversa de la recta r pasará por O y por A´
2. RECTA TANGENTE A LA CPD
La figura inversa de la recta es una circunferencia que pasa por el centro de inversión y por el punto de tangencia con la CPD
3. RECTA SECANTE A LA CPD
La figua inversa de la recta es una circunferencia que pasa por el centro de inversión y por los puntos de corte con la CPD
4. RECTA QUE PASA POR EL CENTRO DE INVERSIÓN.