espaciogeométrico
DIBUJO TÉCNICO PARA SECUNDARIA Y BACHILLERATO.
30/1/25
8/1/25
20/10/24
NORMALIZACIÓN. PEVAU ANDALUCÍA. 2024-2025
ORIENTACIONES Y DISEÑO DE LA PRUEBA 2024-2025
BLOQUE C: NORMALIZACIÓN Y DOCUMENTACIÓN GRÁFICA DE PROYECTOS
Saberes básicos establecidos en el Real Decreto 243/2022, de 5 de abril, del Ministerio de Educación y Formación Profesional y en la Orden de 30 de mayo de 2023 de la Consejería de Desarrollo Educativo y Formación Profesional.
COMENTARIOS:
En los ejercicios correspondientes al bloque de Normalización y Documentación Gráfica de Proyectos se aplicarán las Normas de Dibujo Técnico siguientes:
• UNE-EN ISO 5456-2: 2000. Dibujos técnicos. Métodos de proyección. Parte 2: Representaciones ortográficas. (ISO 5456-2: 1996).
• UNE-EN ISO 5456-3: 2000.Dibujos técnicos. Métodos de proyección. Parte 3: Representaciones axonométricas. (ISO 5456-3: 1996).
• UNE-EN ISO 128-2:2022.Documentación técnica de productos (TPD). Principios generales de representación. Parte 2: Convenciones básicas para las líneas. (ISO 128-2:2022) (Ratificada por la Asociación Española de Normalización en diciembre de 2022).
• UNE-EN ISO 128-3:2022. Documentación técnica de productos (TPD). Principios generales de representación. Parte 3: Vistas, secciones y cortes. (ISO 128-3:2022). (Ratificada por la Asociación Española de Normalización en octubre de 2022).
• UNE-EN ISO 129-1:2019/A1:2021. Documentación técnica de los productos (TPD). Representación de dimensiones y tolerancias. Parte 1: Principios generales. Modificación 1 (ISO 129-1:2018/Amd 1:2020) (Ratificada por la Asociación Española de Normalización en febrero de 2021).























.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)








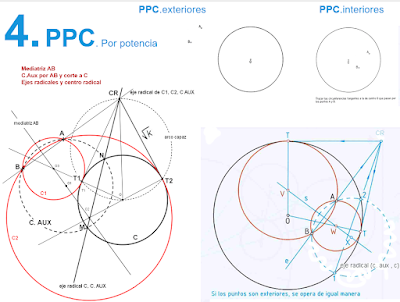
.jpg)

.jpg)
bis3.jpg)
.jpg)



.jpg)

.jpg)
.jpg)
.jpg)
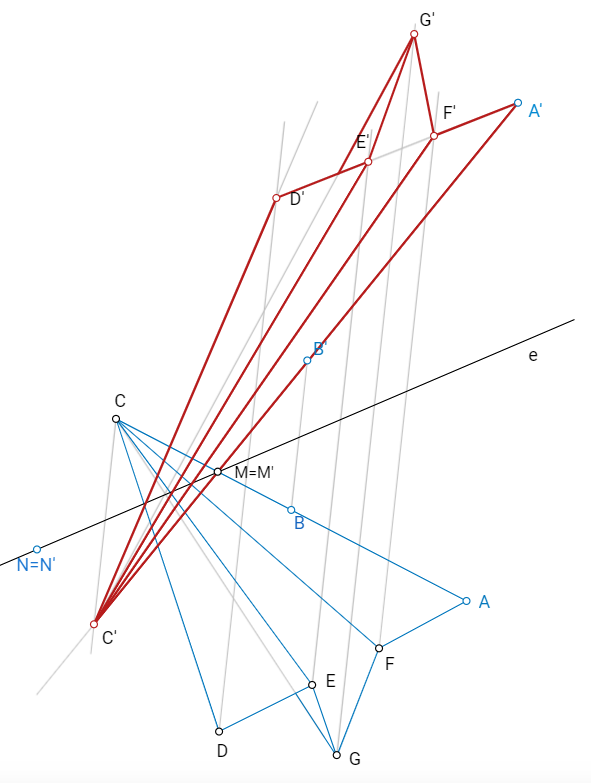
.jpg)
.jpg)