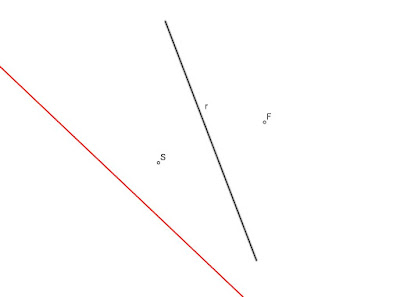
Conocemos que las cónicas son el LG de los centros de las circunferencias que pasando por un foco son tangentes a la CF del otro foco.
Por tanto, tendremos que hallar las circunferencias con centro en la recta r dada, tangentes a la CF de un foco y que pase por el otro foco y su simétrico S
Tendremos que recordar algún caso de tangencias.
INTERSECCIÓN DE RECTA r CON PARÁBOLA
Circunferencia que pasa por dos puntos y es tangente a una recta
Los puntos de corte de la recta con la parábola son centros de las circunferencias tangentes a una recta (d) situados en otra recta r y que pasan por el foco F y su simétrico S.
1-Simétrico de F
2-C Auxiliar con centro en r y pase por S y F
3-MN puntos de corte con C Focal (directriz)
4-El eje radical de la recta directriz d y la circunferencia aux. c, es
la propia directriz. d=e
5-El eje radical de las circunferencias con centro en la curva y
tangentes a la directriz y la circunferencia aux.c es la recta e1
6-Centro radical CR al unir MN y SF ( punto de corte de los ejes e y e1)
7-Al unir los puntos de tangencia T1 y T2 con el otro foco (situado
en el infinito) ,se obtienen los puntos de intersección I1 e I2