PARÁBOLA

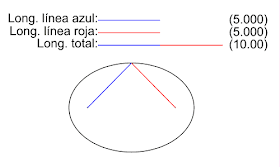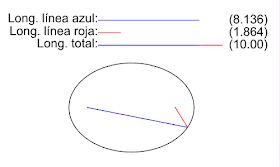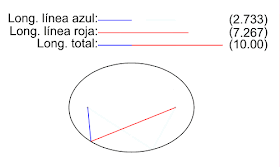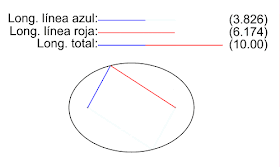
Es el lugar geométrico de los puntos del plano que equidistan de un punto llamado foco y de una recta llamada directriz.

También puede definirse como el LG de todos los puntos del plano que son centros de circunferencias que pasan por un foco y son tangentes a una recta llamada directriz.

HIPÉRBOLA

El plano que secciona al cono es paralelo a dos generatrices

Lugar geométrico de los puntos del plano cuya diferencia de distancias a dos puntos fijos es siempre constante e igual al eje mayor AB (2a).

Se puede definir también como el LG de los puntos del plano que son centros de circunferencias que pasan por un foco y son tangentes a la circunferencia focal trazada desde el otro foco

ASÍNTOTAS

ELIPSE

ELIPSE: Es el lugar geométrico (LG) de todos los puntos del plano cuya suma de distancias a dos puntos fijos llamados focos ( F, F´) es constante e igual al eje mayor AB (2a). PF + PF´= 2A.

También se puede definir como el LG de todos los puntos del plano que son centros de las circunferencias que pasan por un foco y son tangentes a la circunferencia focal trazada desde el otro foco.

CIRCUNFERENCIAS FOCALES: 
Tienen por centro un foco y radio el eje mayor AB=2a
Es el LG de los puntos del plano símetricos de un foco respecto de la tangente a la curva

CIRCUNFERENCIA PRINCIPAL: 
su diámetro es el eje mayor AB.
LG de los puntos del plano que son pies de las perpendiculares desde los focos a las tangentes a la curva

AFINIDAD ENTRE ELIPSE Y CIRCUNFERENCIA


EJERCICIOS ELIPSE. MÉTODOS DE CONSTRUCCIÓN

CURVAS CÓNICAS. TEORÍA

CURVAS PLANAS	CURVAS CÓNICAS	CIRCUNFERENCIA ELIPSE PARÁBOLA HIPÉRBOLA
	CURVAS TÉCNICAS	ÓVALO OVOIDE ESPIRALES VOLUTAS

La línea curva se define como aquella que tres de sus puntos consecutivos, infinitamente próximos, no siguen la misma dirección.

Se define también como el lugar geométrico de las posiciones de un punto móvil en continuo cambio de dirección.

Esta línea es geométrica cuando la trayectoria de sus puntos es continua y establecida por una determinada ley.

Las curvas planas son probablemente las figuras más comunes en la naturaleza y la técnica, por lo que su estudio resulta fundamental para la descripción del entorno.

Gracias al dibujo, se pueden establecer los trazados y las propiedades geométricas de numerosas curvas sin necesidad de aplicar el cálculo infinitesimal.

Las curvas se representan como funciones matemáticas de dos o tres variables que se pueden identificar con los puntos de un plano (coordenadas x  y ) o del espacio tridimensional ( x, y z).

Existen infinidad de curvas planas, algunas de ellas tan caprichosas que no se pueden describir como funciones matemáticas. De entre todas se pueden destacar dos tipos de especial interés: las curvas cónicas y las curvas técnicas.

Superficie cónica

Una superficie cónica es una figura geométrica originada por el recorrido de una recta llamada generatriz, que se apoya en un punto llamado vértice, y en una curva llamada directriz.